Effects of Ambient Temperature on FE Model Updating

Research Team: Babak Moaveni (PI), Iman Behmanesh (grad student)
Funding: NSF-BRIGE (1125624)
Duration: 1/2011 – 4/2012
Relevant publications to date:
Moaveni, B., and Behmanesh, I. (2012). "Effects of changing ambient temperature on finite element model updating of the Dowling Hall Footbridge." Engineering Structures, 43, 58-68.

FE model updating has been extensively used for structural health monitoring. In this method, the physical parameters of a FE model of the structure are updated to match the measured modal properties of the structure as damage evolves, and the updated modeling parameters are used to detect, locate, and quantify damage. The accuracy and spatial resolution of the damage identification results depend significantly on the accuracy and completeness of the identified modal parameters. The focus of this section is (1) to quantify the variation of FE model updating results for the Dowling Hall Footbridge induced by the measured ambient temperatures, and (2) to reduce this variation through removing the temperature effects from identified natural frequencies.

An initial FE model of the Dowling Hall Footbridge is created based on the design drawings and visual inspection of the footbridge, using the MATLAB-based structural analysis software FEDEASLab. Careful attention is paid to model geometry since the dimensions in the design drawings do not exactly match the actual dimensions for a few components of the structure. In the FE model updating process, a limited number of physical parameters of the FE model are updated so the modal parameters (natural frequencies and mode shapes) of the FE model match their experimentally identified counterparts. The updating parameters are the substructure updating factors, which are defined as the relative changes in the effective moduli of elasticity of elements in considered substructures (i.e., groups of elements). In this study, the footbridge is divided into five substructures as shown in Figure 1. The substructures are defined based on the locations of accelerometers.

Figure 1. Considered substructures along the footbridge

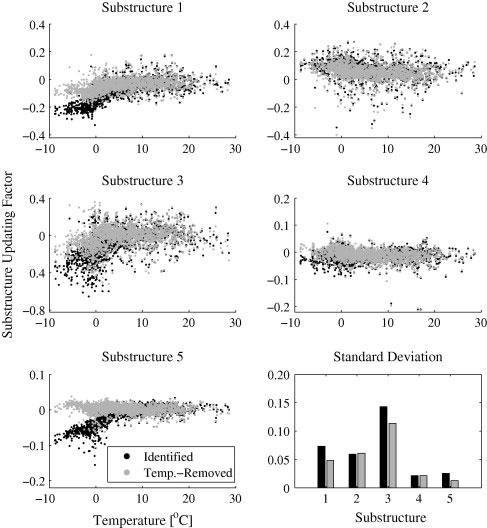
Effects of temperature on the FE model updating are investigated by comparing the results based on two sets of identified natural frequencies: before and after removing temperature effects. The temperature effects are removed from the identified natural frequencies using the above-mentioned fourth-order polynomial regression model. A total number of 2×2,088 = 4,176 model updating runs are performed and the statistics of the substructure updating factors are studied. Figure 2 shows the variation of updating factors versus the measured steel temperature by sensor S3 for both cases of model updating (black dots correspond to before and grey dots correspond to after removing the temperature effects). The variations of updating parameters are reduced after the temperature effects are removed. The standard deviations of three out of five updating factors are reduced up to 50.4%, but the standard deviation of the other two factors remained almost unchanged. It was observed that the reduction in variation of substructure updating factors after removing the temperature effects is significantly less than the reduction in identified natural frequencies (29.7% to 71.3%). Natural frequency residuals of mode 1, 3, and 5 are also significantly reduced after removing the temperature effects. This indicates better fit between the updated FE models and experimental data. Removing temperature effects results in (a) smaller variability in the updated stiffness parameters of FE models, (b) lower natural frequency residuals, and (c) updating factors closer to zero. This yields more accurate results when FE model updating is used for localization and quantification of damage as loss of stiffness. It is worth noting that the non-zero updating factors after removing temperature effects are due to other sources of uncertainty/variability such as FE modeling errors, estimation errors of modal parameters, frequency-temperature modeling errors, and pedestrian traffic on the bridge. Effects of estimation and modeling errors on the FE model updating results can be accounted for in probabilistic model updating procedures such as Bayesian FE model updating.

Figure 2. Variation of substructure updating factors versus temperature of sensor S3 (black dots refer to updating results using identified modal parameters, while grey dots correspond to results using temperature-removed natural frequencies)