Disorder suppresses chaos

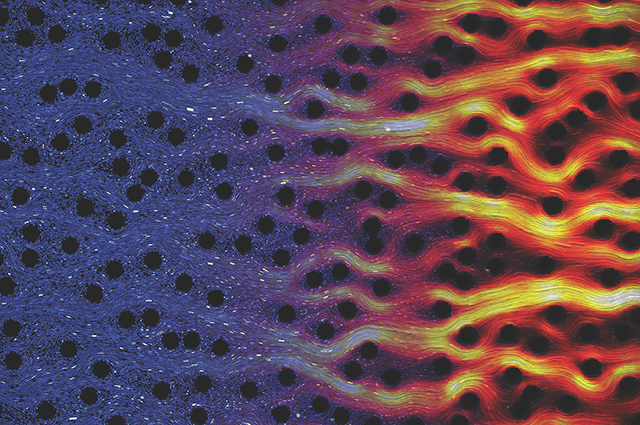
Flow stability is characterized by a fluid’s ability to undergo a minor disturbance, such as a brief change in velocity, and return to its initial state over time. Viscoelastic fluids are often comprised of polymers, which act as springs and impart characteristics of both fluids and solids to the material. Analogous to other non-linear systems, viscoelastic fluid flows can become unstable with ample driving force or stretching, which is characterized by random fluctuations in flow speed.

Unstable flow in viscoelastic fluids can negatively impact a number of applications by creating secondary flows in DNA and blood suspension. Flow instability also makes polymer solutions difficult to pump, which leads to greater power consumption and production costs in polymer processing. Previous microfluidic experiments have characterized viscoelastic flow instability in a range of standard flow geometries, but none have investigated how disorder in the flow geometry affects the stability of viscoelastic flows.

To better understand the relationship between disorder and the onset of instability in viscoelastic fluid flows, researchers from Tufts University, in the Department of Mechanical Engineering and the Department of Physics and Astronomy, performed microfluidic experiments with forests of obstacles (pillar arrays) having various degrees of disorder.

The study, published by Physical Review Letters, found that minor, random pillar displacements (approximately 10% of the pillar spacing) within an otherwise ordered array will stave off the instability to higher flow speeds when compared to a perfectly ordered geometry.

Investigating this result, the researchers designed additional arrays with greater pillar displacements (greater than 25% of the pillar spacing) and observed that large degrees of disorder suppress a viscoelastic flow’s transition to chaos.

The delayed instability and the suppression of chaos is attributed to flow channelization. Channelization enhances the flow along a path of least resistance, which restricts the flow to unidirectional movement and decreases the momentary fluctuations in flow speed. These smoother paths minimize extensional deformation, a primary driver of viscoelastic instability, and promote shear deformation instead. Shear deformation contributes to flow stability by weakly stretching fluid particles and reducing extensional strain as the fluid moves through the pillar arrays.

The team’s study provides a novel, experimental example of the stabilization of a chaotic system via the introduction of disorder. The results emphasize a greater need for understanding viscoelastic flows in complex geometries. Commonly used predictive tools do not fully capture the counterintuitive impact of disorder on viscoelastic flow stability.

Read Disorder Suppresses Chaos in Viscoelastic Flows in Physical Review Letters.